@Paul_Lamb I’m combining your explanations of TM bursting and the TP method we’ve been discussing before.
Sorry for such a long post!
It is known that SP is similar to SOMs in that it reduces the input space, so therefore ‘denoises’ the input, so therefore making it more stable. This is exactly what we want from a TP - in that it forms stable representations over similar inputs. In other words - it ‘generalises’.
A TP cell represents a sequence. The closer the input sequence is to the TP cell’s representation, the greater the TP cell’s activity. This is representative of the cell’s similarity to the input. Naturally most inputs will activate many cells at various levels. The cells with the greatest similarity will have the greatest activity. The cell with the greatest activity will inhibit the cells with lower activity causing a sparse representation of the feature that cell represents.
As discussed before, TP cells get input from column cells. So a TP cell’s potential pool is all the cells in the local columns. Using the same Hebbian learning as SP they learn the sequences of activated predicted cells in the columns. As you’ve visualised above, this looks like a union.
TP cells remain active while their input sequence plays out. Additionally, in this method they increase in activity for as long as they get input. When they lack input their activity drops.

Acceleration, the opposite of adaption
If a TP cell named Q represents the inputs ABCD, then when A is input then Q increases in activity. B is the next input so Q’s activity increases again. The next input is not C, so Q’s activity drops. The next input is also not C nor D so Q’s activity drops again. As Q was active for 50% of the inputs then you could say it was 50% similar to the input sequence. Any cells that had a higher similarity will have a greater activity, so in mutual inhibition they would have inhibited Q’s activity.
I will go over a few examples to demonstrate how this works with different sequences resembling some of the issues we faced in earlier posts.
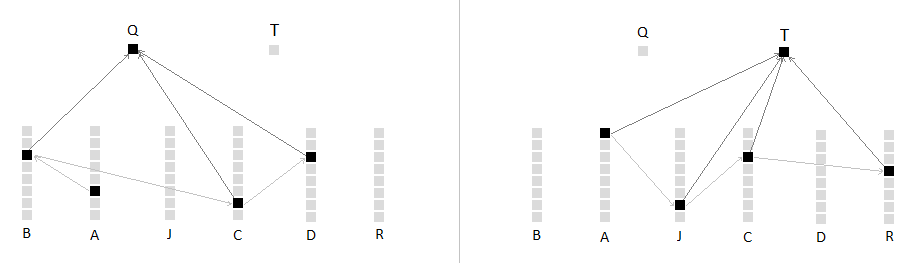
Lets say we have 6 columns for each symbol: B, A, J, C, D, R. We have 2 pooling cells: Q & T. Q represents the sequence ABCD, and T represents AJCR.
Sequence1: ABCDAJCR
This is a simple sequence because it is just a concatination of both sequences that the pooling cells represent. However it is a useful demonstration anyway.
1: Column A bursts and predicts cells in B and J columns. Pooling cells Q and T are equally activated. Because they are both activated they therefore inhibit each other, cancelling each other out.
2: The next input B activates the predicted cell in the B column so therefore activates the Q pooling cell. Q increases in activity while T remains silent from lack of input and from inhibition. Q is winning.
3: Input C will activate a predicted cell that B depolarised causing Q to increase in activity while T remains silent.
4: The same thing happens with input D.
5: Column A bursts and predicts cells in B and J columns. Pooling cells Q and T are equally activated. Due to mutual inhibition Q remains at the same level activity while T remains silent.
6: Input J activates its predicted column cell so therefore contributes activity to T. Q has no input and is inhibited by T, so therefore it looses much of its activity.
7: The same thing happens for input C, except now Q has no activity.
8: The same thing again with T being a clear winner.
This example can be graphed over time:

This shows the winning cell at each step:

So the fast changing sequence ABCDAJCR becomes more stable as the TP outputs QQQQJJJ. This output will in turn become more stable when pooled by the region above.
There is a slight problem. There is a mutual winner on J. Ideally T should be winning on J. So I suspect that activity changes are non-linear. But I’ll stick with linear examples for now.
Sequence 2: ABJCDR
This sequence is a blend of the two TP cell’s representations. We are jumping in and out of each.
1: Column A bursts and predicts cells in columns B & J. A also activates pooling cells Q & T but they mutually inhibit each other.
2: The next input B will activate the cell in column B and activate Q again. Q’s activity increases while T’s remains silent. Q is winning.
3: Next input J column will burst. This activates T while Q drops off. T is winning.
4: Input C activates the predicted cell in column C so therefore the pooling cell T. T is still winning. C did not activate Q because its column cell was not predicted.
5: Input D bursts and simply activates Q. As T did not get any input while receiving only inhibition from Q it will go back to being silent.
6: Input R bursts and simply activates T. T is winning.
The activity of Q and T can be graphed over the sequence:

The blue dots represent the winner at each moment of the sequence:

Q is active 40% of the time (ignoring the mutual inhibition in the first step) while T 60%. This means T is 20% more similar than Q is to the ABJCDR sequence. Of course this may not feel like that (as a human) reading these symbolic sequences. It is likely that is because we are already very familiar with ABCD and not familiar with AJCR. So this kind of suggests that pooling cells have weights (other than permanances) that increase over repetitions of stimuli. Or again top-down biasing can dramatically change the voting outcome.
The main advantage to this TP method is that a TP cell can represent an arbitrarily long sequence. As the sequence progresses the TP cell’s activity increases. This is probably biologically implausible as there are limits to a neuron’s frequency so it should only be able to represent a finite length sequence. But that’s only considering a single cell encoding, not a population encoding.
Anyway that’s the general idea. It’s all about the activity of the TP cell’s activity representing its similarity to the input sequence. I’ve realised there are many other ways to do this. But this is just one way of doing it with HTM’s TM. It has become clear to me tonight that of all the TM and TP methods I have explored (most of which were not posted in this thread) seem to all gravitate towards a core underlying idea. Some methods are more flexible than others. I’ll leave this here as I need to go to bed