Questions on how displacement cells learn movements

Science Related Papers
1

Supplementary material:

For example, if cell G(1,1) is active for a location on an object, a movement one step to the right will cause G(2,1) to become active. Since the cells tile space, an additional movement one step to the right will cause G(0,1) to become active.

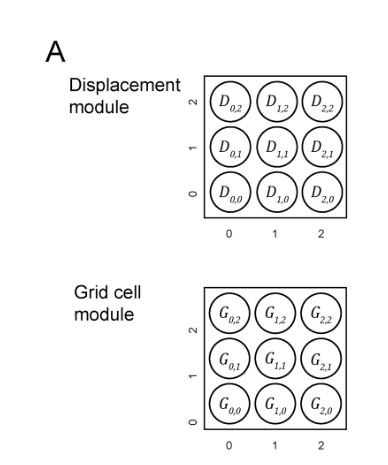
Figure%20A

In the Grid cell module in the Figure A when the cell G(1,1) is active a single step movement can be 1 step to the “left”, “right”, “up”, “down”, “left-up”, “left-down”, “right-up”, “right-down” (diagonally) or “none” (same place but 1 step through time). All these count for 9 displacements of 1 step.

Figure%20B

Figure B shows that independent of which cell performs the 1 step to the right movement D(1,0) will represent the displacement.

Questions:

  1. Can there be displacement cells representing 2,3,n steps?
  2. X
  3. X

Adding to the answer:

This formula in the supplementary material for the 3x3 grid cell lattice example:

G(x1,y1) → G(x2,y2): D((x2-x1) mod 3, (y2-y1) mod 3)

Seems to work for any NxN grid cell lattice and can represent 2,3,n steps.

G(x1,y1) → G(x2,y2): D((x2-x1) mod N, (y2-y1) mod N)

In a 3x3 grid cell module the ambiguity of “4 steps to the right” displacement landing in the same location as the “1 step to the right” displacement is resolved by adding more grid+displacement cell modules. The “4 steps to the right” will be represented by the same displacement cell D(1,0) that represents the “1 step to the right” due to how space is tiled:

N=3: “1 step to the right” => x2 = x1 + 1, y2 = y1

D((x1 + 1 - x1) mod 3, (y1 - y1) mod N)
D(1 mod 3, 0 mod 3)
D(1, 0)

N=3: “4 steps to the right” => x2 = x1 + 4, y2 = y1

D((x1 + 4 - x1) mod 3, (y1 - y1) mod N)
D(4 mod 3, 0 mod 3)
D(1, 0)

4

The example you referred to is a bit contrived because it is so small. In a real space, there might be millions of distinct places you might represent, each one of which could have a displacement applied. But yes, you could have a displacement that represented a jump from any location in space to any other. The steps don’t really matter. Now think about this in a high-dimensional space and :exploding_head:

I don’t quite understand your 2nd two questions, but does my answer help explain anything?

6

It’s probably worth mentioning that ALL mini-columns are potentially responsive grid cells. I don’t think that there are any special structures that you could point to and say “those are the grid cells.”

If you look carefully at the Moser video some cells respond when the animal is in certain locations. Not all at once - just one cell assembly when the animal is in a certain location. The “grid” part is that for a given room the responding mini-column fire when the critter is in a certain external locations that we choose to call a grid. Other cells are also responding but they may be reacting to other locations and spacing or other features. Note that there are cells that respond to things like being close to walls or head direction or speed or elapsed time.

This grid pattern resets to a different organization in a different room. This change in the response pattern is called remapping.

The key point that I am making is that in all the mini-columns that could respond - a given mini-column only responds when the critter is in certain places in the room. Other columns respond to other locations in the room and with different spacing between these locations. As you are thinking about “displacement” and shifting activation go look at the Moser video and try to match that up with the theory. The critter comes from different directions and speeds and still builds the activation pattern.

You might say that what goes on in the EC is special for navigation and I will respond with the concept that the same basic computation is being performed all over the cortex. Cortex is cortex. If you wish to assert that there are different computations being performed then I need some reason why they are different.

The Moser video segment starts at 45 seconds into the grid school lesson, note that this is the response of ONE mini-column. The final collection of dots is all the places in the room that the mini-column was firing. If there were more probes in the brain they would be responding to other locations, spacing, and features.

For you visual learners:

1 Like
7

This is relevant now because some folks are trying to implement displacements for 2D Object Recognition Project.

@nick I have a feeling I did not answer your questions probably because I did not understand them.

Maybe you can restate this question? Do you mean steps in time or steps through the grid?