Why Neurons Have Thousands Of Synapses, A Theory Of Sequence Memory In Neocortex

[subutai]

@nbro

I’m still not sure what mathematical property lets you say that the best you can do is 50%, also because the noise is inserted regularly between the sequences (i.e. at regular intervals, given that the noisy sequences have all the same length, as well as the “normal” sequences) and, after a while, the algorithm should have learned all the sequences.

Each element is represented by an SDR. The SDR is 2048 bits long, with 40 active at a time (each bit here represents one minicolumn). Each noise element is represented by 40 random minicolumns chosen from the 2048 possible. The noise elements are not the same - they are completely different for each timestep. There are a finite number of noise elements, but the number is astronomically large.

[sheiser1]

I think that if a sequence element is random then it couldn’t have been correctly predicted because its not part of a pattern (a recurring sub-sequence). Imagine the case where 100% of the sequence elements were generated randomly. The TM would ultimately learn nothing over time because all the transitions that it did learn were noise and therefore didn’t repeat, so the synaptic permanences representing those transitions would never be reinforced.

A TM with no reinforced paths is a TM that predicts nothing, for 0% prediction accuracy. In summary, the TM can only predict sequence elements it has detected within a pattern, and random/noise elements by definition aren’t.

[nbro]

I partially agree with your reasoning, but there’s a clear repeating pattern in the data, that is

sequence, noise, sequence, noise, sequence, noise, etc

where each sequence has the same number of elements and all noises have the same length. Furthermore, a sequence may repeat.

Here, the confusion/ambiguity is due to the way one defines the prediction accuracy. If one defines the prediction accuracy as the percentage of correctly predicted one-step ahead next input element (either belonging to the sequence or to the noise), then you reasoning makes sense, but the dataset was defined in such a structured way that I’m not seeing why the 50% prediction accuracy mathematically holds…

[sheiser1]

@nbro

If one defines the prediction accuracy as the percentage of correctly predicted one-step ahead next input element

I think this is effectively what they mean by ''prediction accuracy. And yes the “seq., noise, seq., noise…” means that there is repetition to learn from, though only during the seq parts. The other 50% are bouts of noise, so since the TM doesn’t have anything solid to learn from these it wont predict anything during these periods - which would cap the max overall prediction accuracy at 50%. Its like if you were reading something but half of the words were noise (illegible gibberish), the most you could actually make sense of would be the 50% that were real words right?

Btw I also think this demonstrates a great strength of the TM, in that it can learn so aggressively but not be prone to overfitting, since all the noisy transitions it learned at first are washed out since they don’t repeat.

[nbro]

In the section Network Capacity and Generalization, it’s written

The network only learns transitions between inputs. Therefore, the capacity of a network is measured by how many transitions a given network can store. This can be calculated as the product of the expected duty cycle of an individual neuron (cells per column/column sparsity) times the number of patterns each neuron can recognize on its basal dendrites.

A few questions (if you have time to answer @subutai and @jhawkins):

1. What exactly do we mean in this context by “expected duty cycle of an individual neuron”?
2. Why is the expected duty cycle calculated as “cells per column/column sparsity”?
3. Why is the capacity of a network (i.e. how many transitions a given network can store) calculated as “the product of the expected duty cycle of an individual neuron times the number of patterns each neuron can recognize on its basal dendrites.”?

[rhyolight]

You are right that this passage is confusing. The equation for computing capacity is correct but I’m not sure what we meant by duty cycle there. We didn’t really formally define duty cycle for the TM.

If everything is equal, you would expect the average firing rate of a neuron in the TM to be: pct sparsity / number of cells per column. For example, with 2% sparsity and one cell per column, each cell would be active with probability 0.02. With 32 cells per column, each cell would be active with probability 0.000625.

If we are going to call something a “duty cycle”, then it should be 1 divided by (cells per column/sparsity). As written the answer is 1600, but the duty cycle of a cell is actually 1/1600. Although strictly speaking the text is not correct, I don’t think this deserves a correction. The way it was written was to tell the reader what numbers impact the capacity of the network. The answer, 320,000 transitions, is correct. I can see how some readers would be confused, but it is too minor to edit at this point.

[bowen]

so could you please give the exact mathematical equation of calculating the “accuracy” of this figure?

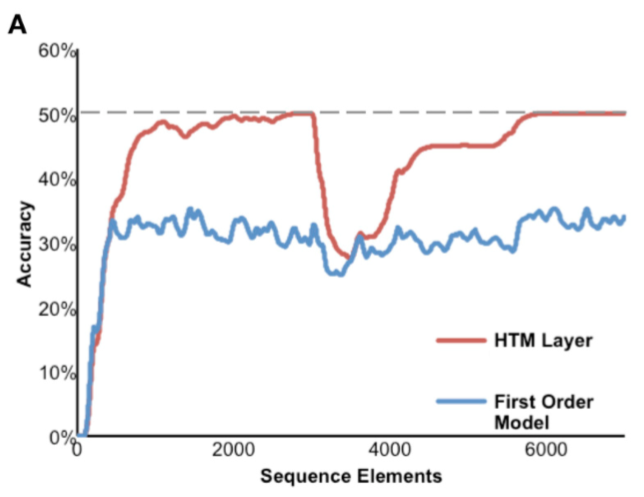
it is indeed confusing. althought I have gone through the previous passages of this topic, I don’t exactly know how tho calculate the accuracy.

[bowen]

@subutai

In this simulation, the stream contained sequences that were each 6 elements long, followed by 4 noise elements. e.g. “XABCDENNNNYABCFGNNNNXABCDENNNN…” (where N is a completely random input).

according to the quote above, I guess we should give the sequence “XABCDENNNN” to TM and see how many times it predicts correctly.

@rhyolight

You know where to look to find this, Subutai just gave you the link.

github.com

numenta/htmresearch/blob/master/projects/sequence_learning/sequence_simulations.py#L122

      nv.add(numpy.random.randint(n))
  noisyVecs.append(nv)


return noisyVecs




#########################################################################
#
# Core experiment routines


def computePredictionAccuracy(pac, pic):
"""
Given a temporal memory instance return the prediction accuracy. The accuracy
is computed as 1 - (#correctly predicted cols / # predicted cols). The
accuracy is 0 if there were no predicted columns.
"""
pcols = float(pac + pic)
if pcols == 0:
  return 0.0
else:
  return (pac / pcols)

while another passage indicate that we should measure the accuracy for each input, i.e. the prediction accuracy = #correctly predicted cols / #predicted cols

so we need a official declare – the exact mathematical equation.

[bowen]

@nbro

accuracy

aha! I know how to calculate the accuracy!

In this paper Continuous Online Sequence Learning with an Unsupervised Neural Network Model, it is illustrated that “prediction accuracy is calculated as a moving average over the last 100 sequences”.