Very nice paper Mark. Thanks for that. That’s the most interesting paper I’ve read in a long time! : - ) I’ve seen very few (if any!) which map language mechanisms to neural connectivity.
I wouldn’t argue with where semantic meaning is stored, especially in the sense of qualia, and the “feeling of being there” which @complyue described as the subjectively intuitive quality of elements we “recombine” when we “think”.
It’s how they recombine which interests me.
Actually, what I’m arguing has a very close analogue in that paper. Exactly figure 2. which you cite as having a resemblance to an RNN below:
Very nice. That figure 2 is work taken from exactly what I identified as the most interesting paper for me cited in that review.
Discrete combinatorial circuits emerging in neural networks: A mechanism for rules of grammar in the human brain? Friedemann Pulvermüller, Andreas Knoblauch
Difficult to find without a paywall, everywhere has scumbag “publishers” trying to clip a ticket… but I finally found it in… Russia! (Bless them for this less violent example of international delinquency!)
https://sci-hub.ru/10.1016/j.neunet.2009.01.009
They say:
“In this present work, we demonstrate that brain-inspired networks of artificial neurons with strong auto-associative links can learn, by Hebbian learning, discrete neuronal representations that can function as a basis of syntactic rule application and generalization.”
Similar to what I’m saying.
And how do they do that:
“Rule generalization: Given that a, b are lexical categories and Ai, Bj lexical atoms
a = {A1, A2, . . . , Ai, . . . , Am}
b = {B1, B2, . . . , Bj, . . . , Bn},
the rule that a sequence ab is acceptable can be generalized from a
set of l encountered strings AiBj even if the input is sparse”
So, I understand this to say, working from the other direction, that given an observed set of encountered strings AiBj, even if it is “sparse”, so not observed for all i and j, you might support other combinations between AiBj, even if they are not observed.
This appears to be is just my AX from {AB, CX, CB} taken from my discussion in this thread above (oh, actually not in this thread? In @JarvisGoBrr 's “elaborator stack machine” thread: The elaborator stack machine - #5 by robf)
It’s all very nice. I hadn’t seen a neural mechanism conjectured on this basis before. And it is very similar to me. (Which is actually not surprising, because the whole distributional semantics idea has been the basis of attempts to learn grammar for years. It’s in their glossary.)
The difference from me seems to be that they conjecture a neural coding mechanism for abstracted categories based on sequence detector neurons. Observed sequences are explicitly coded in sequence detector neurons between word representations, and then categories are abstracted by forming interconnections between the sequence detector neurons. So an abstract syntactic category is represented physically in interconnected sequence detector neurons. This might indeed have a close RNN analogue.
By contrast, while I agree that syntactic categories can be generated from overlapping sets of their AiBj type, this is just distributional semantics, I think those overlapping sets will contradict. That’s the big difference. I think the sets will contradict. So it will not be possible to represent them using fixed sets of sequence detector neurons. Instead I say the “rule” will need to be continually rebuilt anew by projecting out different overlaps between the sequence sets which vary according to context (plausibly, using oscillations to identify closely overlapping sets.)
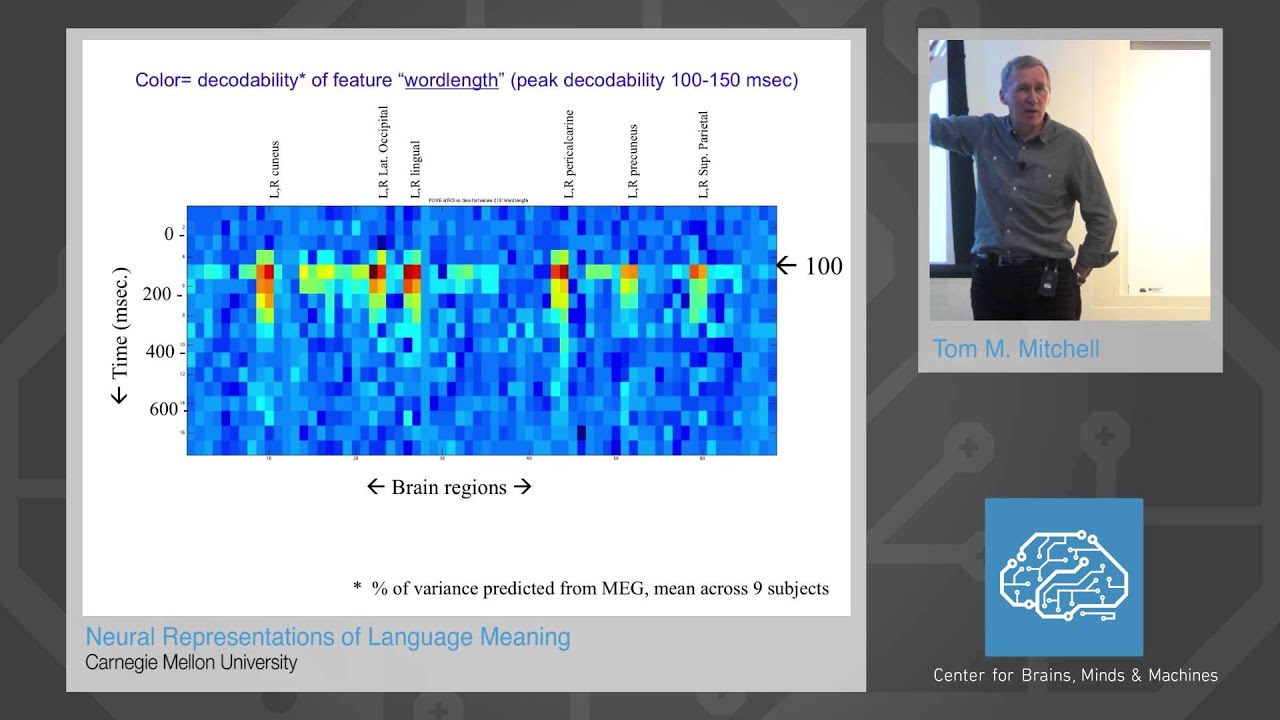
I would justify that constant re-organization idea by citing evidence that neural activations for sequences of words are not static combinations of their individual word activations and any mutual activation between a static set of sequence detector neurons. My favourite example is in work discussed by Tom Mitchell here, the complete reorganization of activation patterns. Surprising! Indicating that patterns of neural activation for word combinations seem to completely re-organize individual word activation patterns:
Prof. Tom Mitchell - Neural Representations of Language Meaning
But the basic idea of a separate “combinatorial semantics” area, where new categories are synthesized by combinations of sets of observed sequences is the same in my thesis and the RNN like mechanism described in this paper. Very nice. Good to see we’re on the same track.
To repeat, the only difference with what I am suggesting, and what is happening in this paper, and probably happening in transformers, is that I say the sets will contradict. So we must model them by finding context appropriate sets associations at run time. Perhaps by as simple a mechanism as setting the sequence network oscillating, and seeing which sets of observed sequences synchronize.
Nobody has imagined contradictory meaning sets before. And they still don’t. Which is holding us back. But trying to abstract language structure drives you to it. If you have eyes to see it. And once you’ve seen these contradictions appear in language structure, you start finding them all over the place. (For instance there’s an analogue in maths. Chaitin: “Incompleteness is the first step toward a mathematical theory of creativity…” An Algorithmic God | Gregory Chaitin | Inference)