The coding of longer sequences in HTM SDRs

[robf]

The issue of coding longer sequences in an SDR has come up in my Chaos and sequential AI models thread with @complyue . That we need to represent letters with SDR, so we can capture code for paths back along a sequence:

Chaos/reservoir computing and sequential cognitive models like HTM

You’re right. With just letters it will be fully connected almost immediately. We need some way to represent that the ends of words will have a greater variety of predictive connections. Perhaps that is just more nodes in the letter representation again. With more nodes in the letter representation we can have paths over different subsets of those nodes representing the context back along the word. And we can have a greater variety of those subsets going out to different first letters of su…

I recall some work done by Felix Andrews @floybix on this, and discussed on the predecessor to this forum, back, initially together with me, starting in 2014. As I recall, basically, making sequence predicting links from only a random selection of nodes in an SDR for a state, could distinguish a path, back, before that state, and onwards, so that the path through that state would be distinguishable in subsequent states too.

This should be important, because the immediate task we are looking at is to represent words as sequences of letters. So we want to have the code for a letter like “e”, in a word like “place”, also be distinct according to the path which arrived at it, through “p”, “l”, “a”, “c”. So, in a way, the SDR for “e” in this context can be distinct, although sharing enough commonality with “e” arrived at in paths through other words, that it can still be identified as a state for “e”.

Firstly, is this something still in HTM? Or if not is there an archive online anywhere for the pre-HTM Formum, NuPIC discussion list where it was discussed?

I’ve been able to find a few links to Felix’s work online. It mostly centered around his port of HTM to Clojure, called Comportex. I see there is still a github repository:

GitHub - htm-community/comportex: Hierarchical Temporal Memory in Clojure

There’s the document on Felix’s continuation of our sequence experiments:
http://viewer.gorilla-repl.org/view.html?source=gist&id=95da4401dc7293e02df3&filename=seq-replay.clj

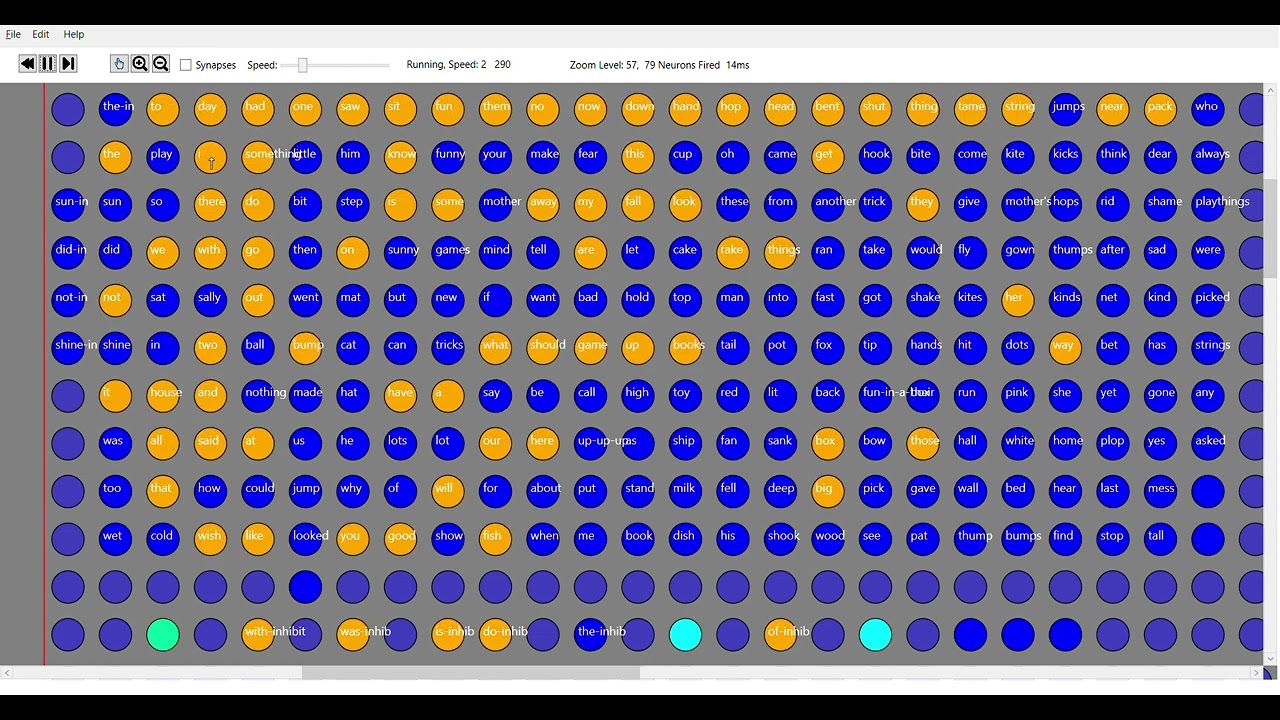
I think this short demo is of the same (in 2016):
HTM higher-order sequence learning - SDRs

HTM higher-order sequence learning - SDRs

There’s also this presentation by Felix at the 2014 fall hackathon. Though it may just be for the Clojure port generally:
HTM in Clojure [DEMO #6] (2014 Fall NuPIC Hackathon)

HTM in Clojure [DEMO #6] (2014 Fall NuPIC Hackathon)

I recall Felix was able to demonstrate the recall of arbitrarily long sequences. It would be good to recover some of those old insights. Or perhaps the current theory of HTM has superseded it??

I don’t suppose @floybix still monitors this forum!

[dmac]

@robf

So we want to have the code for a letter like “e”, in a word like “place”, also be distinct according to the path which arrived at it, through “p”, “l”, “a”, “c”. So, in a way, the SDR for “e” in this context can be distinct, although sharing enough commonality with “e” arrived at in paths through other words, that it can still be identified as a state for “e”.

I think that the temporal memory algorithm should be able to do this.

[robf]

@dmac

@robf

So we want to have the code for a letter like “e”, in a word like “place”, also be distinct according to the path which arrived at it, through “p”, “l”, “a”, “c”. So, in a way, the SDR for “e” in this context can be distinct, although sharing enough commonality with “e” arrived at in paths through other words, that it can still be identified as a state for “e”.

I think that the temporal memory algorithm should be able to do this.

Excellent. Thanks. My memory is coming back. I recall now that patterns of connectivity on dendrites play an important part in locking the state at each time step to its prediction. Each cell in the succeeding state needs a map of the preceding state on its dendrite. That map locks that cell to a prediction, not just by any cell which can predict it, but by only cells of a particular predicting state.

(This came up in some earlier work on an implementation of my whole network generalization thing, where we didn’t notice the dendrite “map”, and every cell activated not only the cells of a state succeeding its state, but the cells of a state succeeding any state it participated in! So it basically predicted everything! Which quickly lit up the entire network!)

Having been taught the importance of this dendrite “map” mechanism, though, I recall I actually came to the conclusion this might be overkill. If there were a mechanism to pool a succession of states, each state wouldn’t need this full map of the preceding state on each of its cells. The pooling method would group the whole sequence together without it.

I wonder if all that is needed is enough distinctness between paths through states. Without the dendrite “map” locking them together.

But from another point of view, this “map” on the dendrites of each cell somewhat IS the pooling method currently implemented in HTM.

Anyway, it drives home the point that connecting successive states with a subset of the SDR for a given state can represent, not only the connection of a state to its preceding state, but also a path to that state at greater distance (the relevant subset in HTM being a subset of the cells in the active columns of a representation.)

Either we will want the full HTM, dendrite “map”, version of that subset connectivity. Or we will find that simply connecting successive states using subsets of a given SDR representation, will give us the diversity for our separate pooling mechanism (synchronized oscillations, I’m hypothesizing) to work.

But this is good. It refreshes my memory how this works in HTM.

That is… I’m understanding this to be saying it’s the entire preceding sequence which encodes each successive prediction. I guess that is implicit in the active state. If there were not a preceding sequence, the columns of the current state would be bursting. So the code captures the entire preceding sequence up until the last “burst”?

There will be a limit to the length of preceding sequence which can be encoded. As stated it reminds me of an RNN. Except it is not trying to generalize each successive state. The point about an RNN is that it is not only recording an entire sequence, but it is trying to generalize over it. To contrast with transformers, this is not selecting which context to pay attention too, or learning combinations of that.

I’m hypothesizing that failure to select or generalize over preceding states to pay attention to, might be fixed in the same way as the need to “lock” the successive states together (by providing a “map” of the entire preceding state for each cell of the entire succeeding state.) The same solution might apply to a mechanism to “lock” the states together, and to identify prior states to pay “attention” to. They would both be aspects of a separate “pooling” mechanism (oscillations in a network?)

[complyue]

I’m still figuring out the ideas toward computer simulation, but feel like to mention local inhibition at the mini-column scope, which is leveraged by HTM sequence prediction. Are we imposing this part or not? HTM inhibition is by design and less inclined to get tuned by hand, I wonder possible conflicts in later steps when we’ll tune inhibition for desirable oscillations.

[robf]

I don’t recall why inhibition is done at the mini-column level in HTM.

Is it to train the sequence pattern?

If it’s to train the sequence pattern I’m guessing we can skip it.

I think we can use inhibition only globally, to tune the global oscillation.

I’m guessing we can skip training for sequences. I’m thinking training is only necessary for sequences in HTM, because in HTM both time-steps and state SDRs are basically arbitrary (even if state SDRs have some “spatial” meaning, in sequence terms they are arbitrary.) That means that in HTM we need some way to tie successive states together, and that is done by “training” the SDR of the prior state on the dendrites of each cell in the successor state (correct?)

In our case however the synchronization process is supposed be the thing which ties successive states together. So the “tying together” (and actually the definition of what a state is, and what a time step is…!) should happen as part of the same synchronization process (though possibly requiring different paths through sub-sets of SDRs for each time a sequence is encountered, to make the internal clustering tighter and ensure synchronization.)

[complyue]

@robf

Is it to train the sequence pattern?

As I understand it, the inhibition speaks for a successfully predicated element (predicated then encountered), and further provide more accurate predication for next element in the sequence. An un-expected element once encountered, fires all neurons in a mini-column (i.e. with no inhibition), speaks for maximal uncertainty in prediction of elements to come next, as consuming way too much biological energy in that sense.

I think if without mini-column scoped local inhibition, we can replace a whole mini-column with a single neuron, yet still get a theoretically equivalent model.

[robf]

@complyue

As I understand it, the inhibition speaks for a successfully predicated element (predicated then encountered), and further provide more accurate predication for next element in the sequence. An un-expected element once encountered, fires all neurons in a mini-column (i.e. with no inhibition), speaks for maximal uncertainty in prediction of elements to come next

Yes, that would change. We wouldn’t be “learning” sequences over time steps anymore. We would be expecting the synchronization process to “select” paths through states, as an equivalent for what “training” does for HTM currently (AND pull them together in time to select the “state”, AND actually, by pulling them together into a “state”, select the sense of what it MEANS to have a “time-step” between states!)

@complyue

I think if without mini-column scoped local inhibition, we can replace a whole mini-column with a single neuron, yet still get a theoretically equivalent model.

The sense of a column representing a state, and cells within the column representing paths between states can stay.

We still want a sub-set of cells in a state to represent different paths associated with different sequences of states.

I don’t know what the exact split would be between columns for states and cells for paths between states. But we would want paths to be represented as some kind of subset of cells for a single state. So the distinction between columns and cells might carry over.

[complyue]

@robf

I don’t know what the exact split would be between columns for states and cells for paths between states. But we would want paths to be represented as some kind of subset of cells for a single state. So the distinction between columns and cells might carry over.

Then we need either some “design” for it, or some “evolutional-strategy”, if supervised-learning (like that in HTM) is dropped off.

[robf]

@complyue

Then we need either some “design” for it, or some “evolutional-strategy”, if supervised-learning (like that in HTM) is dropped off.

I’m seeing the “design” as the synchronization process.

As stated earlier:

@robf

In our case however the synchronization process is supposed be the thing which ties successive states together. So the “tying together” (and actually the definition of what a state is, and what a time step is…!) should happen as part of the same synchronization process

If a sequence of letters has multiple paths through the cells of its constituent columns, then that sequence will tend to synchronize under oscillation. Won’t it? That seems an intuitively clear consequence of having more closely clustered internal paths to me.

Why would a sequence of letters with multiple observed paths through multiple cell sub-sets, not tend to result in that sequence synchronizing under any oscillation?

[complyue]

@robf

I’m seeing the “design” as the synchronization process.

To have a computer simulation, “synchronization” is better considered a “meta design”, i.e. more physical designs (e.g. SDR schema, tunable parameters etc.) have to be derived from it.

[Bitking]

@robf

I don’t recall why inhibition is done at the mini-column level in HTM.

Is it to train the sequence pattern?

There are several types of inhibition cells in the cortex.
As to the type pertinent to your question - Chandelier cells.

Chandelier cell

Chandelier Cells in Functional and Dysfunctional Neural Circuits

These cells “listen” exclusively to the boutons (output from the pyramidal cells soma), and they fire really fast. When the chandelier cell fires it inhibits other pyramidal cells in the immediate neighborhood.
The net effect is the cell that is most sure of its input fires first and the nearby cells are stifled. This is the primary mechanism to enforce sparsity.

Numenta does a rough approximation of this with the k-means portion of the spatial pooler. The primary difference between this and k-means is that the inhibitory cell form a clear local spatial exclusion zone that is a key co-factor in hex-grid formation that is missing in the the Numenta implementation.

Other types of Inhibitory cells work to keep the pyramidal cells balanced on a razors edge, ready to fire.

The inhibitory cells are also involved in learning. These may be a component of the “negative weight” function that @roboto asked about in the Negative Weight thread.
https://www.cell.com/neuron/pdf/S0896-6273(11)00879-8.pdf
and
https://www.cell.com/neuron/pdfExtended/S0896-6273(19)30848-7

[robf]

@complyue

To have a computer simulation, “synchronization” is better considered a “meta design”, i.e. more physical designs (e.g. SDR schema, tunable parameters etc.) have to be derived from it.

Can you envisage what I mean by paths through sub-sets of cells between columns of letter representations?

Basically what exists for HTM now in terms of the raw SDR. But not “trained” on a particular set of cells for each path, only set oscillating by some regular driving sequence, and inhibited by trial and error to the point where the spread of activation oscillates.

So, let’s have the SDR “schema” the same. Just not trained. And likely a different set of cells for each time the same sequence is encountered (resulting in strongly reified sequence paths if a sequence is encountered often, possibly coming down to the same thing in the sense of multiple repetitions equating to “training”.)

What “tunable parameters” do you want? Sure, the number of cells, the number of columns/letter, all those sorts of things likely come down to parameters we would need to “tune”. Just as your observation that 26 columns is far too few immediately “tuned” my expectation to be much higher.

[robf]

@Bitking

There are several types of inhibition cells in the cortex.
As to the type pertinent to your question - Chandelier cells.

Nice. If we can find cell types to fit the functional distinctions we’re making, all the better.

[Bitking]

Have at it!

Cortical%20Neurons%20and%20Circuits.pdf

[DanML]

@robf

spread of activation oscillates

This to me means resonance (in a dynamic network). Is this what you mean?
How will you know when you have achieved ‘oscillation’?

@robf

What “tunable parameters” do you want?

Assuming that was what you meant, then you need to ‘tune’ any network even to achieve oscillation, let alone resonance (when a stable/repeating pattern locks in). This can be achieved in a very large number of ways, and may not always even be possible for any given network - especially if chaotic .

@robf

some regular driving sequence

This sounds like an ‘input frequency’ parameter, and a ‘timeout’ parameter for stabilization. This will also drive the definition of a step (update rate?) or state.

[robf]

@DanML

@robf

spread of activation oscillates

This to me means resonance (in a dynamic network). Is this what you mean?

I think so. I’ve been using the words interchangeably. But resonance will be a maximum on any oscillation. So, another tunable parameter, I guess. Presumably you might vary the inhibition until you got a maximum, and that would be the resonance (about a given driving sequence?)

@DanML

How will you know when you have achieved ‘oscillation’?

Looks like this:

Spontaneous oscillation from a random spike input to a network formed from a small language sample.

Spontaneous oscillation from a random spike input to a network formed from a small language sample.

@DanML

Assuming that was what you meant, then you need to ‘tune’ any network even to achieve oscillation, let alone resonance (when a stable/repeating pattern locks in). This can be achieved in a very large number of ways, and may not always even be possible for any given network - especially if chaotic .

Yes. I thought it would be tricky to get oscillation. I thought some clever feedback connectivity might be necessary. And there may indeed be some tricks remaining to get something meaningful around a specific driving signal from a prompt, such as using subsets of cells to code for sequence. But it turned out that to get a basic network of language sequences oscillating was not hard at all. This is where “suck it and see” can be better than endlessly overthinking it. Playing around with connectivities suggested a solution where I did not expect it.

@DanML

@robf

some regular driving sequence

This sounds like an ‘input frequency’ parameter, and a ‘timeout’ parameter for stabilization. This will also drive the definition of a step (update rate?) or state.

I envisage just a sequence of impulses to the words (letters) of a prompt, in sequence.

Perhaps it will need to drive through many cycles to force the network near a given resonance solution, and maybe some inhibition adjustment together with that.

Then the output should be: the way any network resonance about the driving sequence, pushes the spike time of constituent elements together. Potentially a hierarchy of degrees of being “pushed together”.

[DanML]

@robf

Looks like this:

Spontaneous oscillation from a random spike…

Thanks. That explains a lot.
This looks like a stepped network rather than dynamic to me (all firing states are synchronous). This is a much simpler environment than I was thinking of.

[robf]

@DanML

This looks like a stepped network rather than dynamic to me (all firing states are synchronous). This is a much simpler environment than I was thinking of.

You’re right. Stepped (if that means all states are updated simultaneously?)

It’s done on Charles Simon’s Brain Sim II. Yeah, everything updates simultaneously. And, right again, that will likely make a difference. I hadn’t thought of that. There could still be differences of spike times, but it would be very coarse.

That update schedule is just an artifact of the simulation. Ideally it would all be done on parallel hardware with genuine asynchronous processing. But we should address that on a simulation, yes. Good point.

This was just a basic proof of concept for oscillation. Word connections are single step. No coding of sequences. Lots of refinements needed.

But the underlying principles remain that:

a) oscillation is easy to achieve for language sequences and,
b) tightly interconnected sequences should synchronize

It’s just a matter of figuring out how to squeeze the signal we want out of that (basically that tightness of interconnectivity = equivalent to sharing predictions = finding structure to maximize predictions.)

[complyue]

@robf

Can you envisage what I mean by paths through sub-sets of cells between columns of letter representations?

Details-wise, I’m stuck at “columns of letter representations”, lacking a specification enough concrete.

---

I’m well aware that you are going to tune a lot of things for experimental purpose, but to write a simulation program from scratch, with bare minimum technical debt, I need very concrete specification about what you’d like to start with, and further variations in your mind.

[robf]

@complyue

@robf

Can you envisage what I mean by paths through sub-sets of cells between columns of letter representations?

Details-wise, I’m stuck at “columns of letter representations”, lacking a specification enough concrete.

It’s great that you’re working on it. Many eyes on the same problems finds solutions at multiples of speed.

As you may have guessed, I’m also in a position of “lacking a specification enough concrete”! I’m thinking as I go. Only holding on to the basic insight: that tightness of clustered sequential links should cause synchronization. And at the same time be “meaningful” as (borderline chaotic?) structure which will maximize prediction.

So any more detailed specification I give you will just be my best next guess too.

But, taking that next best guess…

How would HTM currently code for letters? Letters in isolation. If there exists an example of how letters were coded for HTM in the past, we might take that as an initial guess how we want to code them now.

I don’t mean a word representation as was done by cortical.io. I recall those were “spatial” representations (not sequential anyway, as far as I know.) As I recall “spatial” in the sense of a kind of “meaning” distance, so “distance”/space from (non sequential) co-occurrence in texts (Wikipedia, I recall.)

But maybe someone did an experiment using SDR representations for letters some time in the HTM past. Then we could use that.

If not, we needn’t sweat that. Really I think we can try just about any SDR letter representation as a first approximation. Then when it doesn’t work, we figure out why, and try something better. So… Your initial guess of 2000 columns results in a network likely too big to simulate. So why not 200? 200 columns, each with 100 cells. Assign some well distributed random code from those 200 columns to each letter (as a tweak we might cluster them on similarity of sound value, but I don’t think that’s necessary for a start.)

I think that, randomly assigned over 200 columns, code might be enough to start (will 200 columns be enough, do you think?) But as a biological digression your question got me interested in the actual code coming from the cochlea. So I’ve turned up the paper below. I’ll take a look at that. But that may be closer to actual biology than we need to go. I don’t know. I’ll take a look at it. Interesting tangent:

Sound Coding in the Auditory Nerve: From Single Fiber Activity to Cochlear Mass Potentials in Gerbils

Sound Coding in the Auditory Nerve: From Single Fiber Activity to Cochlear...