A month or two ago I set out to train a system to learn representations of objects that are invariant to the type of input given to represent it. I wanted to recreate the way our brains use one representation of the concept of a ‘dog’ regardless of whether we hear a dog, see a dog, or read the word ‘dog’. After expanding my library to allow multiple independent input spaces per pooler, allowing for co-learning across different input dimensions, today I’m excited to share my first small success!
First, I trained an SP on two simultaneous inputs: MNIST handwritten digits, and scalar encoder SDRs matching the actual digit shown on each image (Note to self: this also gives me an idea for ‘supervised’ learning in HTM… I should look into this later). Then I trained a TM, again on simultaneous inputs, with the two sequences [0, 2, 4, 6, 8] and [0, 1, 2, 3, 4, 5].
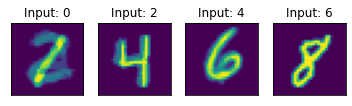
Then, I tested the TM by providing only the scalar encoder inputs–no images–and attempted to reconstruct what the TM ‘thought’ would be the next input as an image by comparing the predictive cell SDRs at each test step to the active cell SDRs in the training stage and using a simple KNN approach. The results are very promising.
Quick block-diagram for illustration:
Test sample on sequence 1 : [0,2,4,6,8].
Test sample on sequence 2: [0,1,2,3,4,5]

Unsurprisingly, it’s sometimes confused when the initial 0 input arrives because it doesn’t know whether a 1 or a 2 should follow. But the subsequent predictions are almost always correct.
Since the image inputs were not provided during the test stage, I believe this is evidence that the TM and SP have learned invariant representations of the digits. Not invariant to rotation, translation etc. (that wasn’t the goal of this experiment) but invariant to the ‘sense’ that was used to experience the digit.
