Learning, predicting and naming sequences

Community Lounge
1

The idea is to learn a collection of named sequences, and then when you input a fragment of a curve name and predict which one it belongs to. The hypothesis is that the brain is doing something similar. For example, say you start spelling out a word: ‘f’, ‘fr’, ‘fro’, … With just an f it could be any word with an f in it. Then ‘fr’ narrows it down a little. Then ‘fro’ narrows it down further. Eg, to ‘frog’, or ‘from’ or etc. But it applies to floats and integers too. Say you start with 3. This could belong to almost any sequence/curve right? But what if the next symbol is ‘.’. And the next is 1. Suddenly you would predict Pi: 3.141592… Now what about floats? An example I like is playing football. Someone kicks the ball a long way, and your brain is trying to predict where it will fall so you can catch it. The hypothesis is that you have seen the football fall so many times that you have a big collection of stored sequences of falling football positions. As it falls, the number of matching predictions shrinks, until you know enough to get in the right position and catch the thing. It certainly seems more plausible the brain is doing this than solving some physics equation.

Now on to some worked examples:

Input a decimal point, and we get Pi and e:

$ ./seq2name.py '.'
float_sequence:
input sequence: ['.']
name  similarity  prediction
----  ----------  ----------
Pi    100         . 1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4
e     100         . 7 1 8 2 8 1 8 2 8 4

Input Fibonacci but with a couple of minor errors:

$ ./seq2name.py 1 1 2 3 5 7 13 21 36
float_sequence:
input sequence: [1, 1, 2, 3, 5, 7, 13, 21, 36]
name       similarity  prediction
----       ----------  ----------
Fibonacci  44.271      1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
counting   6.541       2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
Pi         5.237       2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6 4 3 3
counting   4.259       1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Pi         2.112       2 6 4 3 3 8 3 2 7 9 5
e          1.689       1 8 2 8 1 8 2 8 4
factorial  1.562       1 1 2 6 24 120 720 5040 40320 362880 3628800
Pi         0.872       3 2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5
Pi         0.778       1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6 2 6
Fibonacci  0.488       1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
Pi         0.455       1 4 1 5 9 2 6 5 3 5 8 9 7 9 3 2 3 8 4 6
factorial  0.423       1 2 6 24 120 720 5040 40320 362880 3628800
Pi         0.42        2 3 8 4 6 2 6 4 3 3 8 3 2 7 9 5

Learn two simple sentences: “boys eat many cakes” and “girls eat many pies”, then input a sentence fragment:

$ ./seq2name.py eat
float_sequence:
input sequence: ['eat']
name           similarity  prediction
----           ----------  ----------
boy sentence   100.0       eat many cakes
girl sentence  100.0       eat many pies
boy sentence   16.667      cakes
alphabet       16.667      a b c d e f g h i j k l m n o p q r s t
alphabet       16.667      e f g h i j k l m n o p q r s t u v w x
alphabet       16.667      t u v w x y z
boy sentence   11.111      many cakes
girl sentence  11.111      many pies
girl sentence  11.111      pies

Now a sentence fragment with a typo:

$ ./seq2name.py eats mnay
float_sequence:
input sequence: ['eats', 'mnay']
name           similarity  prediction
----           ----------  ----------
boy sentence   55.556      eat many cakes
girl sentence  55.556      eat many pies
boy sentence   11.111      boys eat many cakes
boy sentence   9.722       many cakes
girl sentence  9.722       girls eat many pies
girl sentence  5.556       many pies
alphabet       5.556       a b c d e f g h i j k l m n o p q r s t
alphabet       5.556       e f g h i j k l m n o p q r s t u v w x
alphabet       5.556       s t u v w x y z
alphabet       5.556       t u v w x y z

Now on to pretty pictures:
Here are the simple curves we have learnt (trivial to add more to our collection):

Now input a short curve:

$ ./seq2name.py 0 0 2 2 2 2
float_sequence:
input sequence: [0, 0, 2, 2, 2, 2]
name      similarity  prediction
----      ----------  ----------
square    96.875      0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
triangle  8.704       0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28 0.2 0.12 0.04
sin       8.46        0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141
sin       8.435       0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239
sin       8.366       0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042
sin       8.271       0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058
sin       8.221       0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335
triangle  7.912       0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28 0.2 0.12 0.04
sin       7.534       0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427
triangle  7.252       0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28 0.2 0.12 0.04
sin       6.761       0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058 -0.158
sin       6.366       0.0 0.1 0.199 0.296 0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946
zero      6.25        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
zero      6.25        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
zero      6.25        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
zero      6.25        0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Producing these predictions:

Now input a longer curve:

$ ./seq2name.py 0 0 2 2 1.5 1.5 1.6 1.7 1.4 1.5 1.1 1.1 1.1 1.3 1.2 1.9 1.7 1.7 1.6 1.5 1.8
float_sequence:
input sequence: [0, 0, 2, 2, 1.5, 1.5, 1.6, 1.7, 1.4, 1.5, 1.1, 1.1, 1.1, 1.3, 1.2, 1.9, 1.7, 1.7, 1.6, 1.5, 1.8]
name      similarity  prediction
----      ----------  ----------
square    59.236      0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
sin       19.732      0.0 0.1 0.199 0.296 0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946
sin       18.779      0.1 0.199 0.296 0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909
sin       16.873      0.199 0.296 0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863
sin       13.248      0.296 0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808
sin       11.295      0.389 0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746
sin       9.429       0.479 0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675
sin       6.947       0.565 0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598
triangle  5.421       0.0 0.08 0.16 0.24 0.32 0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52
sin       5.293       0.644 0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516
triangle  3.897       0.08 0.16 0.24 0.32 0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44
sin       3.502       0.717 0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427
triangle  3.084       0.16 0.24 0.32 0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36
sin       2.462       0.783 0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335
triangle  2.276       0.24 0.32 0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28
sin       1.718       0.841 0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239
triangle  1.587       0.32 0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28 0.2
sin       1.302       0.891 0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141
triangle  1.192       0.4 0.48 0.56 0.64 0.72 0.8 0.88 0.96 1.04 0.92 0.84 0.76 0.68 0.6 0.52 0.44 0.36 0.28 0.2 0.12
sin       0.846       0.932 0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042
sin       0.609       0.964 0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058
sin       0.38        0.985 0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058 -0.158
sin       0.268       0.997 1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058 -0.158 -0.256
sin       0.166       1.0 0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058 -0.158 -0.256 -0.351
sin       0.12        0.992 0.974 0.946 0.909 0.863 0.808 0.746 0.675 0.598 0.516 0.427 0.335 0.239 0.141 0.042 -0.058 -0.158 -0.256 -0.351 -0.443

Producing these predictions:

Now learn some simple paths:

Now input the starting point (1,1):

$ ./seq2name.py '(1,1)'
float_sequence:
input sequence: [(1, 1)]
name    similarity  prediction
----    ----------  ----------
path a  100.0       (1, 1) (1, 2) (1, 3) (2, 4) (3, 4) (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)
path b  100.0       (1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1) (6, 2) (5, 3) (5, 4) (5, 5) (6, 5) (7, 6)
path c  100.0       (1, 1) (1, -1) (0, -0.7) (-2.5, 3.2) (-4, 2.1) (-5, 5) (-7, 3) (-8, 0)
path a  8.269       (1, 2) (1, 3) (2, 4) (3, 4) (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)
path b  8.269       (2, 1) (3, 1) (4, 1) (5, 1) (6, 1) (6, 2) (5, 3) (5, 4) (5, 5) (6, 5) (7, 6)
path c  0.034       (0, -0.7) (-2.5, 3.2) (-4, 2.1) (-5, 5) (-7, 3) (-8, 0)
path a  0.031       (1, 3) (2, 4) (3, 4) (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)
path b  0.031       (3, 1) (4, 1) (5, 1) (6, 1) (6, 2) (5, 3) (5, 4) (5, 5) (6, 5) (7, 6)

Producing these predictions:

Finally, input a short path:

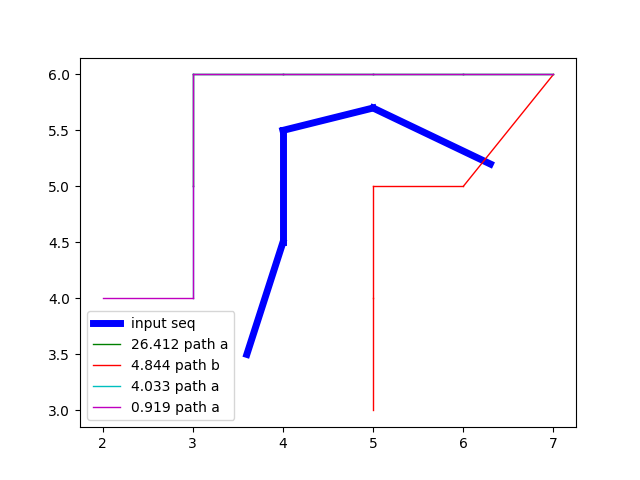
$ ./seq2name.py '(3.6,3.5)' '(4,4.5)' '(4,5.5)' '(5,5.7)' '(6.3,5.2)'
float_sequence:
input sequence: [(3.6, 3.5), (4, 4.5), (4, 5.5), (5, 5.7), (6.3, 5.2)]
name    similarity  prediction
----    ----------  ----------
path a  26.412      (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)
path b  4.844       (5, 3) (5, 4) (5, 5) (6, 5) (7, 6)
path a  4.033       (3, 4) (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)
path a  0.919       (2, 4) (3, 4) (3, 5) (3, 6) (4, 6) (5, 6) (6, 6) (7, 6)

Producing these predictions:

Code here.

2

Next part of my code, given a sequence, name the sub-sequences (with some tolerance for noise). Here is our example input sequence, where the 7’s serve as an anomaly:
input_seq = sequence(‘input seq’) + zero + square + triangle + sin + [7,7,7,7,7,7,7,7,7] + triangle + square + zero
This is what it looks like:

Here are the predicted names of the subsequences:

$ ./seq2name.py
seq2name:
100.0 zero,     100.0 square,   100.0 triangle, 100.0 sin
100.0 zero,     93.017 sin,     93.017 triangle,        50.0 square
100.0 zero,     89.718 triangle,        89.718 sin,     25.0 square
100.0 zero,     88.076 triangle,        88.076 sin,     12.5 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
56.25 square,   50.0 zero,      44.038 sin,     39.077 triangle
81.25 square,   25.0 zero,      22.429 sin,     20.885 triangle
93.75 square,   12.5 zero,      11.951 sin,     11.788 triangle
100 square,     8.46 sin,       8.453 triangle, 6.25 zero
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100 square,     50.054 triangle,        50.054 sin
75.0 square,    71.555 triangle,        71.555 sin
75.775 sin,     75.757 triangle,        55.517 square
77.429 triangle,        76.789 sin,     42.706 square
90.398 triangle,        83.213 sin,     77.927 zero,    6.35 square
100 triangle,   89.525 sin,     68.844 zero,    6.413 square
100 triangle,   98.254 sin,     58.401 zero,    5.709 square
100 triangle,   99.127 sin,     47.739 zero,    19.119 square
100 triangle,   100 sin,        38.795 zero,    15.206 square
100 triangle,   100 sin,        33.913 zero,    15.437 square
100 triangle,   100.0 sin,      27.516 zero,    11.535 square
100 triangle,   100 sin,        21.697 zero,    9.149 square
100 triangle,   97.381 sin,     16.257 zero,    7.043 square
100 triangle,   95.687 sin,     12.279 zero,    7.912 square
100 triangle,   98.254 sin,     10.038 zero,    8.453 square
100 triangle,   96.61 sin,      10.515 zero,    9.321 square
100 triangle,   96.508 sin,     13.375 zero,    11.472 square
100 triangle,   95.636 sin,     14.874 zero,    10.898 square
100.0 triangle, 97.381 sin,     18.339 zero,    13.137 square
100 triangle,   98.254 sin,     24.189 zero,    16.491 square
100 triangle,   99.127 sin,     31.208 zero,    20.053 square
100 triangle,   99.127 sin,     40.019 zero,    25.162 square
100 triangle,   93.89 sin,      44.588 zero,    24.866 square
100 triangle,   96.508 sin,     52.426 zero,    30.21 square
100 triangle,   98.254 sin,     62.913 zero,    36.648 square
100 triangle,   99.127 sin,     74.815 zero,    43.14 square
100 triangle,   100 sin,        87.392 zero,    50.054 square
94.038 zero,    93.002 triangle,        93.002 sin,     3.747 square
90.446 zero,    83.986 triangle,        83.165 sin,     4.573 square
84.392 triangle,        82.083 zero,    79.065 sin,     5.449 square
97.379 triangle,        86.905 sin,     71.357 zero,    6.397 square
100 sin,        98.254 triangle,        60.095 zero,    6.576 square
100 sin,        99.127 triangle,        48.56 zero,     5.929 square
100 triangle,   100 sin,        38.795 zero,    15.206 square
100 triangle,   100 sin,        33.913 zero,    15.437 square
100 sin,        100.0 triangle, 27.516 zero,    11.535 square
100 triangle,   100 sin,        21.697 zero,    9.149 square
100 sin,        93.89 triangle, 18.878 zero,    9.664 square
100 sin,        97.381 triangle,        15.099 zero,    7.279 square
100 sin,        92.196 triangle,        12.958 zero,    7.803 square
100 sin,        95.687 triangle,        10.465 zero,    7.37 square
100 sin,        98.254 triangle,        9.382 zero,     8.221 square
100 sin,        95.687 triangle,        8.677 zero,     8.271 square
100 sin,        87.853 triangle,        8.46 square,    8.458 zero
100 sin,        90.539 triangle,        8.284 square,   8.284 zero
100 sin,        92.4 triangle,  8.292 zero,     8.284 square
100 sin,        96.61 triangle, 9.806 zero,     9.795 square
100 sin,        93.257 triangle,        10.561 zero,    9.04 square
100 sin,        92.196 triangle,        10.943 zero,    8.662 square
100 sin,        96.508 triangle,        13.752 zero,    11.094 square
100 sin,        97.381 triangle,        17.872 zero,    13.141 square
100 sin,        95.636 triangle,        19.838 zero,    12.564 square
100 sin,        98.254 triangle,        24.844 zero,    16.299 square
100 sin,        99.127 triangle,        31.535 zero,    19.957 square
100 sin,        99.127 triangle,        40.346 zero,    25.066 square
100 sin,        96.508 triangle,        50.054 zero,    30.332 square
100 sin,        98.254 triangle,        61.727 zero,    36.709 square
100 sin,        99.127 triangle,        74.132 zero,    43.158 square
100 triangle,   100 sin,        87.392 zero,    50.054 square
100 sin,        87.039 zero,    86.034 triangle,        3.747 square
100 sin,        80.364 zero,    72.898 triangle,        4.558 square
100 sin,        70.458 zero,    59.761 triangle,        5.377 square
100 sin,        60.064 zero,    48.83 triangle, 6.248 square
100.0 sin,      53.995 zero,    43.364 triangle,        5.375 square
100 sin,        45.521 zero,    35.887 triangle,        4.554 square
100 sin,        37.26 zero,     28.845 triangle,        3.733 square
100 sin,        29.175 zero,    21.476 triangle,        3.05 square
100 sin,        22.853 zero,    16.562 triangle,        3.05 square
100 sin,        19.351 zero,    13.941 triangle,        2.367 square
100 sin,        15.069 zero,    10.565 triangle,        1.864 square
100 sin,        12.928 zero,    9.432 triangle, 1.361 square
100 sin,        10.435 zero,    7.448 triangle, 1.033 square
100 sin,        9.352 zero,     6.597 triangle, 1.033 square
100 sin,        8.647 zero,     6.308 triangle, 0.706 square
100 sin,        8.458 zero,     6.212 triangle, 0.706 square
100.0 sin,      8.269 zero,     6.169 triangle, 0.517 square
100.0 sin,      8.269 zero,     6.169 triangle, 0.517 square
100.0 sin,      8.269 zero,     6.169 triangle, 0.517 square
100 sin,        9.779 zero,     7.679 triangle, 0.517 square
100.0 sin,      10.535 zero,    8.434 triangle, 0.517 square
100 sin,        13.533 zero,    11.247 triangle,        0.517 square
100 sin,        15.032 zero,    12.099 triangle,        0.517 square
100 sin,        18.497 zero,    15.14 triangle, 0.706 square
100 sin,        24.159 zero,    20.571 triangle,        0.706 square
100 sin,        27.153 zero,    22.355 triangle,        1.033 square
100 sin,        32.511 zero,    27.223 triangle,        1.033 square
100 sin,        40.819 zero,    34.985 triangle,        1.361 square
100 sin,        50.526 zero,    43.307 triangle,        1.864 square
100 sin,        61.697 zero,    53.942 triangle,        1.864 square
100 sin,        74.102 zero,    64.765 triangle,        2.367 square
43.017 sin,     37.392 zero,    27.229 triangle,        3.05 square
20.108 sin,     19.038 zero,    14.938 triangle,        3.733 square
10.806 sin,     9.929 zero,     9.11 triangle,  4.554 square
6.25 sin,       5.375 zero,     5.375 square,   5.375 triangle
ANOMALY
ANOMALY
ANOMALY
ANOMALY
ANOMALY
ANOMALY
ANOMALY
ANOMALY
ANOMALY
100 triangle,   89.525 sin,     68.844 zero,    6.413 square
100 triangle,   98.254 sin,     58.401 zero,    5.709 square
100 triangle,   99.127 sin,     47.739 zero,    19.119 square
100 triangle,   100 sin,        38.795 zero,    15.206 square
100 triangle,   100 sin,        33.913 zero,    15.437 square
100 triangle,   100.0 sin,      27.516 zero,    11.535 square
100 triangle,   100 sin,        21.697 zero,    9.149 square
100 triangle,   97.381 sin,     16.257 zero,    7.043 square
100 triangle,   95.687 sin,     12.279 zero,    7.912 square
100 triangle,   98.254 sin,     10.038 zero,    8.453 square
100 triangle,   96.61 sin,      10.515 zero,    9.321 square
100 triangle,   96.508 sin,     13.375 zero,    11.472 square
100 triangle,   95.636 sin,     14.874 zero,    10.898 square
100.0 triangle, 97.381 sin,     18.339 zero,    13.137 square
100 triangle,   98.254 sin,     24.189 zero,    16.491 square
100 triangle,   99.127 sin,     31.208 zero,    20.053 square
100 triangle,   99.127 sin,     40.019 zero,    25.162 square
100 triangle,   93.89 sin,      44.588 zero,    24.866 square
100 triangle,   96.508 sin,     52.426 zero,    30.21 square
100 triangle,   98.254 sin,     62.913 zero,    36.648 square
100 triangle,   99.127 sin,     74.815 zero,    43.14 square
100 triangle,   100 sin,        87.392 zero,    50.054 square
94.038 zero,    93.002 triangle,        93.002 sin,     3.747 square
54.558 square,  47.429 zero,    46.501 sin,     39.733 triangle
80.377 square,  24.125 zero,    23.25 sin,      20.226 triangle
93.748 square,  12.498 zero,    11.949 sin,     11.786 triangle
100 square,     8.46 sin,       8.453 triangle, 6.25 zero
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100.0 square,   8.269 sin,      7.225 triangle
100 square,     50.054 triangle,        50.054 sin
75.0 square,    71.555 triangle,        71.555 sin
80.651 triangle,        80.651 sin,     62.5 square
84.372 triangle,        84.372 sin,     56.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square
100.0 zero,     87.392 triangle,        87.392 sin,     6.25 square