Most frequent SDR overpowering all other bits

Engineering
, ,
1

Looking for advice.

It’s been very intriguing for me to learn about the specific property of SDRs: that despite the limited amount of bits (let’s say 20 out of 4000), the number of things it can uniquely represent is ginormous, given by the combination formula.

Expectation

In theory, different SDRs that are reusing some bit positions should never matter, because it’s the overall signal strength that matters (overlap will be very small).

For a concrete example, I’ve been trying to create a heteroassociative memory to remember “Hello world” string

INPUT = character position (layer #1, I generate different positions for each)

OUTPUT = SDR of the letter (layer #2)

Now, let’s say I have these input SDRs:

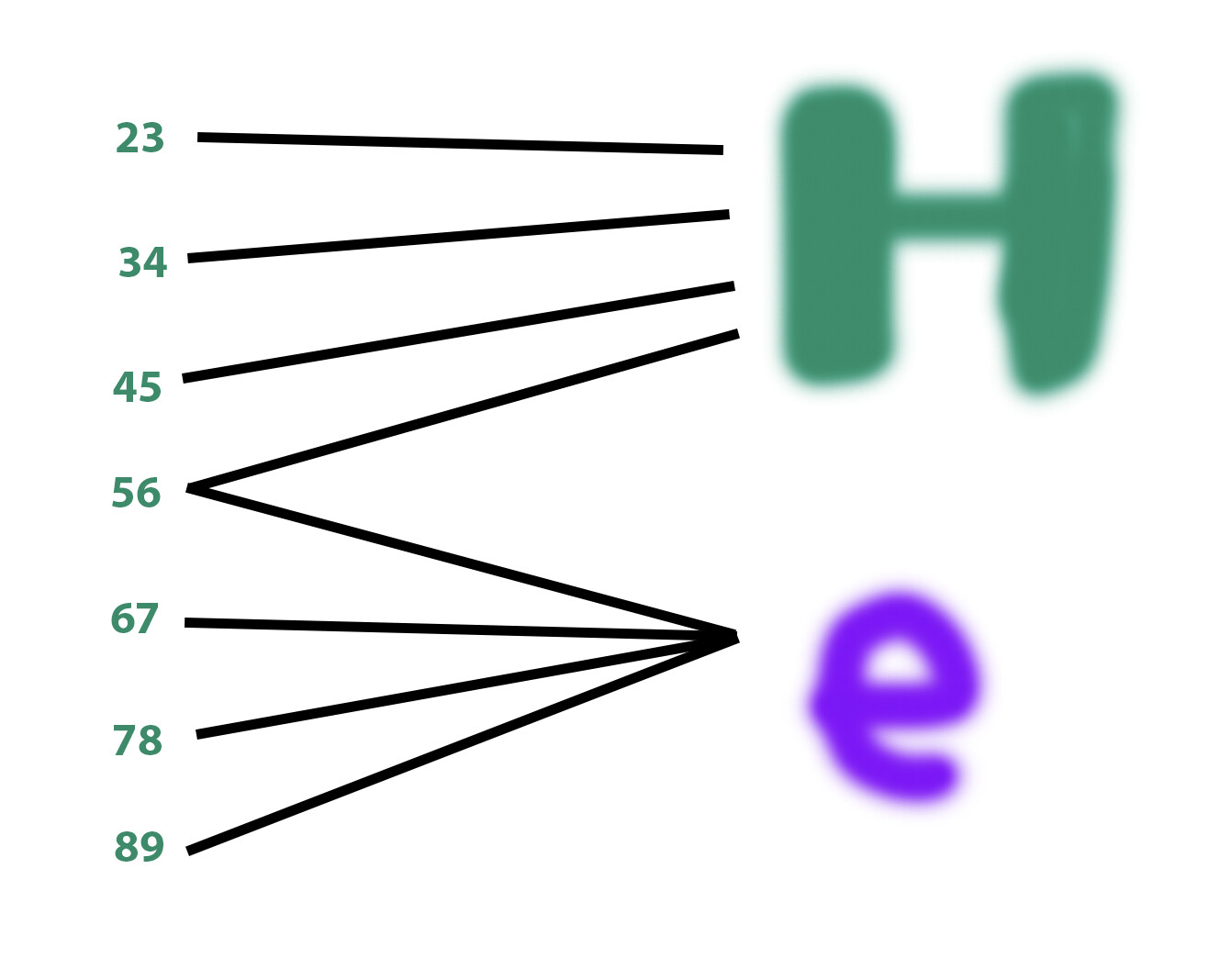
0th position → bits (23, 34, 45, 56)
1st position → bits (56, 67, 78, 89)

And I boost the connections from (23, 34, 45, 56) to SDR of the letter “H” in the output layer

…and (56, 67, 78, 89) to the letter “e”, and so on.

The theory says, it shouldn’t matter that 56 was accidentally selected to be used to encode both positions 0th and 1st

If 23, 34, 45 and 56 become set in the input layer at “inference” time, the signal to “e” will be so faint it’s almost non-existent, because the signal to “H” should overpower, so we get our “H” back correctly.

And of course, with more bit width of the SDR, the effect is even better. Which allows for all these crazy amount of combinations that all overlap with each other because of the limited amount of bits available, but every time we can recover the signal for the specific input because it will appear “brighter”, and the rest will be faint noise.

Reality

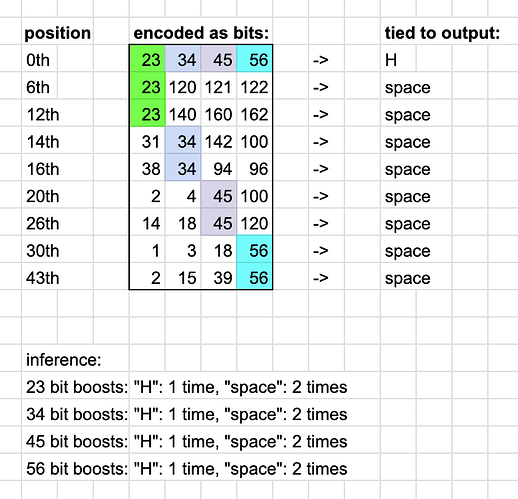
Here’s where the problem starts in practice, the one I’ve ran into. Let’s say some output letter in the text we’re trying to memorize is used more often than the rest - in practice, this pesky character turned out to be a space character.

Intuitively it should still be unclear why it would present a problem at this moment. But let’s consider the case where the bit level capacity = 200 bits to choose from, we choose 15 bits each time, and what happens after 1000 characters are stored.

Out of the 1000 characters, we encountered the space character, let’s say, 100 times (10% frequency). This means that for 100 different text positions (memory cells), which were assigned their all unique 15-bit SDRs, we boosted the connection from those bits to the space character SDR in the output layer. So now we had 100 positions * 15 bits = 1500 bit choices got connected to the space output SDR.

Of course, we don’t have 1500 input bits, we could only select them each time from the pool of 200, so each input bit 0…200 got ~7.5 boosts on average to the space character in the output layer.

Now, when we try to do “inference”, what happens?

image
image722×696 62.6 KB

Let’s consider again (23, 34, 45, 56…) SDR for 0th position. The letter expected is “H”

However, each of those input bits (23) (34) (45) (56)… separately, in the context of different unrelated input SDRs, got strongly connected to the space character with ~+7.5 weight, and only 1.0 to “H”

As a result, the output brightly highlights the SDR for the damn space almost every time! When I try to read back the text, it reads back space in almost every position.

Any thoughts on how this could be solved? I can obviously just make the output SDR be dependent on input SDR with hashing (so the SDR for “H” will also be different depending on the position), and I can even decode it back successfully - makes the memory almost perfect - but I don’t think that’s biologically plausible at all, where the output (some action, let’s say) has to be encoded differently, surely not. The closest I think I got to a candidate solution is pattern separation in hippocampus, but I don’t know if anyone tried something like this when applied to SDRs.

1 Like
2

Hi,

In the original HTM systems: the synapse weights saturate at 1.
In fact there are only two possible weights: 0 and 1.
Synapses are either fully connected or not connected at all.

You haven’t really described how your synapses work, but would this help solve your issue?

1 Like
3

If you want to encode an 1000 chars long text in a 4000 bits SDR in a way that is useful for downstream ML tasks, I don’t think it works that way.

1 Like
4

Thank you for the ideas

In my original implementation here, the issue is that the weights from “pos.1” SDR bits to “H” is something like 1.0, and the weights from “pos.1” SDR bits to [space] is something like 37.8 (since every individual bit of “pos.1” SDR, separately, inside other SDRs, was tied to the space multiple times.

So I have weights to “H” and [space]: (1.0, 37.8)
If I make all weights snap to 1 when we have a connection, pretty soon most of the weights will become 1, because for each input bit you could find connections to almost any other output bit. So I get (1.0, 1.0)
If I clip the weights at 1, I still get (1.0, 1.0) instead of (1.0, 37.8)

And what I would like to have is (1.0, 0.0042) or something. And for this, the only way I’m seeing is that SDRs are not enough, somehow pattern separation needs to occur on a few more hidden layers. Meaning that there are neuron SDRs on hidden layers that only respond to “pos.1” input SDR somehow, and suppress the rest

Basically, the problem is that in practice, SDR bits are leaking into each other (bits of one SDR, activated within separate SDRs, still affect that SDR in a strong way) which I didn’t expect when I was going over theory.

It works perfectly once I “salt” the output SDR with the input bits, making one conditional on the other – then I’m able to recover megabytes of text perfectly (closer to the theoretical information theory capacity of the storage; recall that the connection storage space is quadratic and the storage type is float), similar to my experiments with Kanerva memory. So this makes me think that this touches somehow on fundamental properties of SDRs (or at least in naive implementations with one layer) - being prone to frequency bias/oversaturation/whatever we might call it.

By salting/hashing, I mean that in the original version, I predefine the output alphabet SDRs for each ASCII character once for the whole text, but in the salted version, I permute alphabet SDRs in a deterministic way based on the position. So space character SDR that I could find at 5th position is completely different from space character SDR at 10th position, and so they don’t have the chance of clumping together and saturating the weights with this pattern. When I recover it back, I apply the permutation back. And the storage capacity is insane again, just like I hoped.

But I don’t think this hashing/salting is biologically plausible. Mapped to a brain, this would be analogous to the following situation: a school teacher gives a child a table of 10x10 characters to remember in one hour. Half of those characters are the letter “X”. When the teacher returns, the child is unable to store the table in memory, and erroneously recalls 99% of the table as “X”, instead of only 50%. Because when the teacher asks “position (5,4)”, the connections from (row=5) and (col=4) to the correct letter “D” were boosted only once, but there there were several (5,_) that pointed to “X” - let’s say (5,0), (5,3), (5,6), (5,7) and (5,9), and there were several (__,4) that pointed to “X” - (2,4), (3,4), (7,4), (8,4) and (9,4)

It’s not the best example because one could argue that we would use phonological loops, grid cells as locations and other clues to remember the table, but the point still stands, somehow introducing a frequent output class that we remember doesn’t wipe out all other classes just because it’s the most frequent and all bits in all other SDRs were tied to it many times over. Even in grid cells, food or danger being present in 30% of locations would wipe out the contents of all other cells.

This doesn’t happen of course, so somehow the brains are smarter than this.

2 Likes
5

I still have problem understanding how the downstream task (or memory) is processing these SDRs,

One (possibly unsuccessful) idea would be to partially replace a high frequency letter with high frequency letter pairs which begin with same letter.
E.G if most frequent successor of “t” is “h”, make “th” a separate symbol.

The point is to substitute the original alphabet with a much richer and statistically uniform alphabet, which will spread bit collisions uniformly.
An added benefit would be a shortening of the original sequence length.

The large SDR allows for a gazillion of sub-encodings.

PS

I don’t think kids work that way, unless tortured into make a prediction they will output a honest “I don’t know”. Or if they-re smart will try memorizing positions of letters that aren’t an X. Otherwise said - consider the X-es as background

And maybe come up with the idea of focusing on learning each of the four 5x5 squares in which the 10x10 image can be patched.

These are some clues on why visual transformers are effective: by using some kind of patching and attention.

1 Like
6

I’m gonna share my code below, but basically, my goal was to empirically confirm my intuitions about the properties of SDRs.

The final goal is to attempt to harness their power to build alternative systems to GPTs. I didn’t use full HTM framework because there are some things that are not biologically plausible, such as the artificial cutoff of sparsity at 2% instead of natural synaptic homeostasis/free energy principle/whatever, as long as it’s biologically plausible (I’ve been working on spiking NN simulations trying to make the dynamics as close to natural as possible). However, a lot of inspiration can be drawn from HTM theory, and I feel that Jeff’s and Matt’s enthusiasm about SDRs was definitely spot on and is indeed a very important clue to figuring out intelligence.

At the moment, I’m just investigating the general capacity of SDRs to store information, similar to Kanerva memory. I basically shove as many bits into a system as I can and see at which point it starts to saturate.

Very good suggestion! Alas, a few issues:

  1. Now the alphabet is of ginormous length, and I have to store the alphabet together with the memory (mapping of the multi-character tokens to their SDRs, to then compare the predicted output)
  2. It has the same weakness as what GPT-4 suggested the other day – normalizing via dividing by frequency – in that it is biologically implausible: I can’t know beforehand which output class will be high frequency, and the brain certainly doesn’t go and mathematically divide every synapse value after it learns about it
  3. Later on, the output class might be its own entity (a concept of a cat, a signal to “go left” in an reinforcement learning agent, a concept of danger “there be dragons”, and so on). And I don’t want a situation where “there be dragons” overpowers 99% of SDRs just because this situation is encountered frequently (~20%). And the suggestion is basically to split the output into several (“there be danger, and you will be eaten” vs. “there be danger, and you will get your food taken” are completely different SDRs), but this will fail to generalize, because I’d like the agent to learn in both situations “what to do if there’s danger” → “run”). My code (Experiment #3) does something similar to your suggestion, only instead of salting the output with extra characters, it salts it with the input position (a@pos0 and a@pos1 are different SDRs). It works perfectly, but, this breaks the generalization in the same way, and is not biologically plausible.
  4. “th” is still one of the highest frequency character pairs in English (even the triplet “the”), so I would have to split that further and further and further as well

Yep, it was not the perfect metaphor, but I hope it gets the idea across - we can pick “there be dragons” neuronal group instead of “X” character. I don’t think it’s sharded into millions of SDRs in our brains (well it kinda is because it has different flavors attached and is invoked from different angles, but the core neuronal group activating is still the same I believe, which allows for generalization)

→ “Background” is a concept that is represented as one specific SDR → it gets popular and overpowers all the other outputs because of high frequency → system explodes.

My code:

Really appreciate the ideas and suggestions btw!

2 Likes
7

I wonder what happens if you ignore it - I mean do the shifting/permutation you normally do at every new symbol, without inserting the blank char.
Which would mimic how kids handle backgrounds.

1 Like
8

I’m afraid the second most frequent character would become the problem (as you can see from the code output, e@0, t@0 and [space]@0 are the primary troublemakers)

I actually do have a sense of “I already looked for my glasses at my desk, and it was empty” “I already looked for my glasses on the sofa, and it was empty” and so on and so forth, and I don’t think “it was empty” feeling is pointing to different kinds of empty (would be difficult for me to remember and tie them together in this sentence otherwise). Had I simply ignored the empty value and not inserted it into memory, I would have had “Have I looked at my desk already? No idea, no memories of it, positive or negative”

1 Like
9

My understanding is that for sequences you need multiple layer feed forward of activations to differentiate SDR’s within sequences. I think it’s in one of Matt’s videos.
Have not read the code through thouroughly so may be still misunderstanding some of it.
Within your code the softmax the input boosting is not capped so it allows a singular repetitive bit to end up dominating and attenuating all the other participating bits. This might be your issue.
Wihtin the boost connection, rather than using a string pattern for the connections (very CPU heavy) use a math function to derive a numerical key for the connection and use that as the key in the lookup, much faster if you use say a 64bit int as its a single memory value / instruction per operation.
Remember that the SDR actually stores nothing, it’s just an access key / trigger.

1 Like
10

Thanks for looking into it @BrainVx!

Makes sense. In my case, I’m not treating the text as a sequence, but rather a random access memory (character position → character)
Actually, maybe it can even store sequences in just two layers if we make a character “salted” (conditional) on a few previous ones, I’ll need to check.

Softmax turns a “soft” SDR, reading activations at the output layer after setting input bits, [ 0.0, 0.0, 0.0, 0.0, 37.0, 0.0, 0.0, 0.0, 1.0, 0.0, 1.0, 37.0, 37.0... ] into probabilities summing up to 1, i.e. [ 0.0, 0.0, 0.0, 0.0, 0.333333, 0.0, 0.0, 0.0, 0.333333, 0.0, 0.333333, 0.000001, 0.000001... ]

Unfortunately, 37.0 is projecting the highly boosted pattern for the space character, and 1.0 pattern is the real character stored at this position. So the problem occurs even before softmax.

Oh yeah, good optimization. I need to benchmark it, since the hashmap should just turn the key into an int64 hash anyway and supposed to be O(1) operation for both store and lookup, but direct int64 keys should indeed be faster.

1 Like
11

I just glimpsed over the code, I still don’t get it what model (which is fed in learn(key_sdr, value_sdr)) is supposed to achieve:

  • a simple auto associative memory (kanerva like) where it is shown an sdr representing a letter and returns a “cleaned up” variant of that letter.
  • or it is shown a sdr encoding a juxtaposition (or sequence) of letters and returns… what?
  • or a next letter predictor (as Temporal Memory) when fed in the beginning an initial sequence of SDRs

?

PS a couple more questions:

  • is the model fed with the big text then the queries are run for shorter 30 or 400 letter sequences?
  • or it is cleared after each test and then it sees only a short (30 or 400 long) sequence which then latter attempts to reproduce?
1 Like
12

Heteroassociative memory
Input (layer 1) = character position in text (every position index is encoded as a separate SDR)
Output (layer 2) = the character at that position

In Kanerva, that would be hypervector address => data

Training: Input and Output patterns are projected, connections between these bits are strengthened by a simple increment
Inference: Input pattern is shown at L1, trying to read out the character using the projected activations pattern at L2

is the model fed with the big text then the queries are run for shorter 30 or 400 letter sequences?

Correct, first the training for 30 or 400 characters, then inference reading them back one by one

It’s never shown the full 1MB here, but in my other tests it does work and recovers 99.9% of it.

Each of the 3 experiment runs clears the model first. Then training, then inference.

The only difference between experiment 2 and experiment 3: output character SDRs become differentiated based on positions. Massive difference in results (but need to store the alphabet of 256*400 SDRs instead of 256 SDRs, which is enormous)

2 Likes
13

Fwiw, Kanerva’s capacity:

HARD_LOCATIONS 8192
LIMIT = 8192 characters: incorrect: 109 / 8192 (1.3%)
LIMIT = 81920 characters: incorrect: 15493 / 81920 (19%)

Notes from running capacity experiments with SDRs:

Robustness experiments
* Not having out_sdr predicated on in_sdr was a total mess, after 4000 chars it was already destroyed by space character (0x20)
* 1M chars, 4096 N, 41 W (1%) -> 27% inaccurate
* 1M chars, 4096 N, 82 W (2%) -> 59% inaccurate
* 1M chars, 4096 N, 21 W (0.5%) -> 16% inaccurate
* 1M chars, 4096 N, 5 W (0.1%) -> 16% inaccurate
* 1M chars, 8192 N, 81 W -> 0.1% inaccurate
* 1M chars, 8192 N, 41 W (0.5%) -> aaalmost 0% inaccurate (2/50000 on last batch)
* 1M chars, 8192 N, 9 W (0.1%) -> 0% inaccurate (0/400000 on last batch)
* 100k chars, 2048 N, 20 W -> 0.2% inaccurate
* 1M chars, 4096 N, 41 W -> 82% inaccurate
* 10M chars, 8192, 9 W (0.01%) -> 60% inaccurate
* 10M chars, 8192, 5 W (0.005%) -> 63% inaccurate

Increasing W does increase running time. Probably even superlinearly, need to check

Decreasing W improves accuracy dramatically, but it also shrinks capacity
2 Likes
14

Thanks, it is more clear now.

That sounds quite cool, how big the model itself is (or it gets to be if it expands dynamically)? I mean how many “parameters” , “weights”, or whatever metric you use?

1 Like
15

Connections are N bits in the input to N bits in the output, so maximum storage is N^2

2 Likes
16

From my own experiments with associative memories on SDRs, and also from testing Triadic Memory (heavily discussed on a topic here), the problems arises when keys collide aka overlap. Random SDRs encoding position are fine.

1 Like
17

Yeah I’m controlling for that

image
image1998×812 94.9 KB

The overlap is rare enough that the salted version gives a perfect score, so it’s not that

Quite sure the problem is in the naivety of my boosting stage, not in the encoding, i.e. there should be something more sophisticated than just doing +1 per connection on each step. Maybe I need to look into inhibition as well

I was also thinking – home come deep neural networks don’t have the same problem? There must also be cases where some output class (like a space token) is dominating the dataset. Then I realized, they likely do run into this problem, and the network quickly learns to cheat and output the most frequent class, but then the training keeps going, gradient descent pushing it more and more, and the network starts to become more nuanced, first learning bigram statistics, and then more and more sophisticated.

Not sure if I’m a fan of this, because if I want biologically plausible online learning, I don’t want to give the network the same information over and over and over until it learns it, that’s not how humans do. But that’s the problem with DNNs, they can’t learn from one mention of a fact, because the learning rate, being a fraction of 1.0, is slowly turning the dials, so the network has to be exposed to the same data again and again and again until it learns that e.g. Linda Yaccarino is now CEO of Twitter, not Jack Dorsey, and oh btw, it’s now X. Somehow humans outperform it with just 1-2 shot learning.

Will look into triadic stuff, thanks

2 Likes
18

I just skimmed through the post so excuse me if it’s already discussed but

  1. Have you tried updating the permanences instead of directly updating the weights by \text{weight}_{i,j} = H(\text{permanence}_{i,j} - \text{threshold}), where H(\cdot) is the unit step function, by incrementing/decrementing the permanences akin to the SP learning rules?
  2. Have you tried experimenting with something like Gibbs sampling the Hopfield network update rule on the value layer through the lateral connections?

In SDRs, by principle, a single bit should not have a significant semantic meaning. So it doesn’t make sense to allocate large weights to one.
Lateral connections may increase the capacity, but at an additional cost indeed. However, it might become redundant if you introduce a better overlap algorithm.

EDIT: I was confusing optimization with sampling.

1 Like
19

I was saying “that” will become an issue for problems where there will be no longer so easy to map keys (as it was to map position in your case) to random SDRs.

E.G. Think of how would be used your associative memory having MNIST image as keys being mapped to class (0…9 values) prototypes. It’s easy to project “values” from 0 to 9 to random SDRs in order to avoid value collision but not so for the actual images.

1 Like
20

This is quite a popular assertion. If it were true, all first graders would be able to learn multiplication table up to 10, or the alphabet letters, in no more than 1-2 lessons.
We have a pretty good short term recollection of experiences/thoughts/talks we’ve been passing through, but remembering/integrating them for long term requires much more than a couple exposures to an arbitrary stimulus and I’m sure there is a lot of background post-processing which very likely involves some form of unconscious repetition.

1 Like